La question semble innocente et pourtant… Parmi les trois diagrammes triangulaires, lequel vous semble le mieux représenter la répartition « 50% – 50% » ?
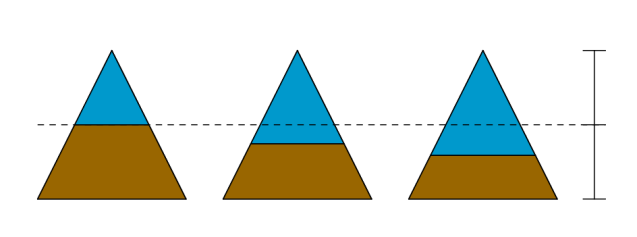
Vous avez choisi le premier diagramme ? Vous raisonnez donc en termes de longueurs : puisque l’on veut représenter des répartitions égales, il faut couper le diagramme à la moitié de la hauteur.
Vous avez opté pour le troisième diagramme ? Vous raisonnez cette fois par les surfaces. Les surfaces bleues et marron sont en effet égales, mais pour cela, il a fallu que la hauteur du triangle bleu atteigne environ 70.7 % de la hauteur totale (√2 /2 pour être plus exact).
Vous avez privilégié le deuxième ? Votre oeil vous a sans doute guidé car c’est peut-être le diagramme le plus convaincant esthétiquement parlant. Néanmoins, il ne possède aucune propriété mathématique simple qui permette de justifier que ce diagramme pourrait représenter une répartition égale entre deux caractères. Vous avez été dupé(e), et vous ne serez sans doute pas le dernier ou la dernière !
Longueurs et surfaces
Prenez un carré. Si vous multipliez la longueur de ses côtés par 2, la surface délimitée par ce carré sera alors multipliée par 2 x 2 = 4. Si vous multipliez les longueurs par 3, la surface sera maintenant multipliée par 3 x 3 = 9.
De fait, si on souhaite multiplier la surface d’un carré par 2, il faut multiplier la longueur de ses côtés par √2, soit environ 1.414.

Le carré de droite a une aire deux fois plus grande que le carré de gauche.
Cela semblera innocent pour ceux d’entre vous qui sont familiers avec ces notions, mais elles peuvent facilement déconcerter. A titre personnel, j’ai été surpris par l’allure du troisième triangle dessiné plus haut, bien que sachant parfaitement que son découpage était équitable. L’oeil m’a trompé, mais les maths m’ont ramené à la raison.
A titre d’autre exemple, voici une cible « équitable » : chaque anneau possède la même aire – et il en est de même pour le disque central.

Et en volume ?
En volume, l’illusion est encore plus frappante. En effet, lorsque l’on multiplie les longueurs des côtés d’un solide par 2, le volume de ce solide est multiplié par 2 x 2 x 2 = 8. Ceci marche évidemment pour n’importe quel nombre.
Ainsi, si je souhaite construire une pyramide dont le volume est 2 fois moins important qu’une pyramide donnée, je dois diviser les longueurs par la racine cubique de 2, soit environ 1.26.
Pour reprendre l’illustration du premier sondage de cet article, si je faisais une petite pyramide imbriquée dans une deuxième de manière à avoir 50% du volume total contenu dans la petite pyramide, la hauteur de cette petite pyramide serait égal à environ 80% de la hauteur totale. Et puisqu’une image vaut mieux qu’un long discours…

Le volume de la pyramide bleue est égal au volume du socle marron.
Jetons également un oeil à un découpage de pyramide en 10 tranches égales. Si le bas du solide ne semble pas contraire à notre intuition, le haut peut nous confronter un sérieux doute…

Quand la sphère joue des tours
Histoire de terminer sur une bonne note, allons voir du côté de notre amie la sphère. Découpons la sphère en plusieurs parts de hauteur égale, comme ceci :

Si, évidemment, le volume de chaque tranche de la boule est différent, tout s’arrange lorsque l’on s’intéresse à la surface. En effet, la surface d’une bande sphérique ne dépend que de la hauteur de celle-ci ainsi que du rayon de la sphère. Elle ne dépend pas de l’endroit où se trouve cette bande !
Enfin, cela dit, qui aurait l’idée de représenter des données à l’aide d’un diagramme sphérique.


