π est juste, oubliez τ !

Attention, cet article peut contenir : Mauvaise foi (75%), Hooliganisme piiste (3.14%)

Nous sommes au IIIe siècle avant notre ère, au temps où Archimède tente d’exprimer le rapport entre la circonférence d’un cercle et son diamètre. Ces calculs le mènent à un nombre compris 220/71 et 22/7. Des siècles plus tard, nous savons antre autre que ce fameux nombre noté π ne peut s’écrire sous la forme d’une fraction. Et il s’avère que ce petit π a fait bien du chemin, loin de son cercle : on le voit apparaître dans de nombreuses autres formules de géométrie mais aussi d’analyse ou d’algèbre.

Seulement voilà, π est le rapport entre la circonférence et le diamètre du cercle, mais tout mathématicien vous répondra que l’important dans le cercle, ce n’est pas le diamètre, mais bien le rayon ! Après tout, le cercle n’est-il pas l’ensemble des points situés à une distance donnée d’un point donné ?

Ceci pris en considération, la circonférence C du cercle s’exprime en fonction du rayon R comme étant C = 2πR. Et c’est ce 2 qui fait grincer des dents ! Parce que quitte à définir une constante pour le cercle, autant faire en sorte qu’elle ne soit pas accompagnée d’un autre constante à côté – ce fameux 2 ! Pire encore, il semblerait que notre nombre π, dont on a dit qu’il s’aventurait et visite de nombreux domaines des mathématiques, ne puisse se séparer de son petit facteur 2 si encombrant.

Un clan obscur s’est alors formé pour établir une nouvelle constante du cercle : plutôt que d’utiliser π, ceux-ci recommandent d’utiliser son double, τ = 2π.

Deux articles se font alors les manifestes de ces tauistes :

• π is wrong, de Bob Palais, en 2000
• Le Tau Manifesto de Michael Hartl, en 2010

Vous pouvez allez lire ces lignes si vous le souhaitez, je me charge de vous les faire oublier dans celles qui vont suivre.

π et le cercle

Drapeau vert : Cette partie ne demande aucune connaissance mathématique particulière

Pourquoi diable Archimède a-t-il défini π ainsi ? Pourquoi n’a-t-il pas directement calculé le rapport C/R, qui vaut environ 6.28. La raison ici est purement technique : prenez un objet circulaire dont vous ne connaissez pas le centre.

Pour déterminer son diamètre, il suffit de prendre deux droites parallèles, de rapprocher ces deux droits jusqu’à bien encadrer l’objet puis de mesurer l’encadrement. Pour mesurer le rayon… Et bien il faut d’abord calculer le diamètre, puis le diviser par 2.

En d’autres termes, pour les objets du quotidien, le diamètre est la quantité la plus accessible. Pas étonnant donc que les largeurs des vis ou des balles de fusils expriment le diamètre plutôt que le rayon !

π se retrouve ailleurs avec le cercle, puisque pour obtenir l’aire d’un cercle de rayon R, il faut faire le calcul A = πR². Nul besoin d’un 2 ici. Alors oui, je sais, d’un coup, je suis d’accord pour utiliser le rayon plutôt que le diamètre, ce qui rend la formule plus jolie. Je vous répondrai simplement que, dans les deux cas, l’utilisation de τ aboutira à des formules peu aguichantes.

En résumé, π et τ peuvent être définis ainsi :

 

Il y a de quoi donner de la constante du cercle à chaque nombre. Alors voyons plutôt du côté des angles.

Angles et polygones

Mesurer des angles en degré, c’est depuis bien longtemps dépassé. Les vrais mesurent leurs angles en radian. La règle est simple : 180°, c’est-à-dire un demi-tour, valent π radians, et le reste s’obtient simplement par proportionnalité. L’idée derrière ce changement d’unité est de relier la valeur de l’angle à la longueur de l’arc de cercle que cet angle intercepte : ce doit être la même valeur, au rayon près.

La longueur de l’arc de cercle est égal au produit du rayon et de l’angle mesuré en radians.

Ainsi, si dans un cercle de rayon 1, on choisit deux rayons formant un angle a, alors l’arc de cercle intercepté par cet angle aura une longueur qui vaut exactement a.

Le chemin pour τ semble alors tout tracé : quel est l’angle qui permet de définir un quart de cercle ? τ/4 ! Celui qui définit un tiers de cercle ? τ/3. A côté, π/2 et 2π/3 ne semblent pas offrir de belle résistance.

Des angles en radians… selon Pi ou Tau ! Image de tauday.com

Est-ce suffisant pour autant ? Dites-moi alors l’aire d’un demi-disque unité ? π/2 ! D’un quart du disque unité ? π/4 ! Là encore, τ et π se partagent les lauriers : l’un semble plus adapté aux longueurs, l’autre aux aires. Match nul.

Aires du disque unité. Images provenant de http://www.thepimanifesto.com/

Mais revenons-en aux angles, si vous le voulez bien. Il existe un théorème que vous avez entendu au tout début de votre scolarité : dans un triangle, la somme des angles vaut 180°, autrement dit π radians. Dans un quadrilatère, cette somme vaut 2π radians. Pour un pentagone, 3π radians, pour un hexagone, 4π radians. Pour un polygone à n côtés, elle vaut (n-2)π radians. N’est-ce pas là une formule des plus élégantes ?

Mieux encore, l’aire d’un polygone régulier inscrit dans un cercle de rayon 1 vaut :

Ah oui tiens, je ne vous ai pas parlé de cosinus et de sinus encore ? Il est temps de réparer cette erreur.

Un peu de trigonométrie

Drapeau jaune : Cette partie demande quelques connaissances mathématiques et un peu d’abstraction pour être entièrement saisie.

Prenez un cercle de rayon 1 et tracez deux diamètres perpendiculaires : l’un horizontal, l’autre vertical. Prenez alors un rayon de ce cercle : celui-ci forme un certain angle a avec le rayon horizontal qui part vers la droite. Regardons alors les coordonnées du point d’intersection de ce rayon choisi avec le cercle. Ceux-ci ne dépendent bien évidemment que de l’angle. On appellera alors cosinus de a (noté cos(a)) sa coordonnée selon l’axe horizontal. Son sinus (sin(a)) sera sa coordonnée selon l’axe vertical.

Comme un dessin vaut parfois bien mieux qu’une explication, en voici un :

Puisque faire un tour complet ne change pas le sinus ou le cosinus (ou autrement dit, pour n’importe quel x réel, sin(2π+x) = sin(x) et cos(2π + x) = cos(x)), on aurait tendance à se dire que remplacer π par son cousin serait une bonne idée. Cependant, sinus et cosinus cachent également d’autres formules faisant intervenir π sans être associé à un 2. Pour n’importe quels x réel et n’importe quel entier k, on a en effet.

• sin(π+x) + sin(x) = 0
• sin(π – x) = sin(x)
• cos(π – x) + cos(x) = 0
• cos (π + x) + cos(x) = 0
• sin(kπ) = 0
• cos(kπ) = (-1)^k

On peut également définir, lorsque le cosinus d’un angle ne vaut pas 0 (ce qui arrive avec une période de π), la tangente de l’angle : tan(x) = sin(x)/cos(x). On aboutit alors à de nouvelles identités :

• tan(π + x) = tan(x)
• tan(π – x) + tan(x) = 0

De belles formules, n’est-ce pas ? Mais attendez, car de belles formules, en voilà d’autres !

Des formules élégantes

Drapeau rouge : Cet article demande quelques connaissances mathématiques intermédiaires ainsi qu’une bonne capacité d’abstraction

Les tauistes ont tendance à trouver le 2 qui accompagne π inélégant, inapproprié : c’est d’ailleurs toute la motivation de ce mouvement. Mais ce couple est-il omniprésent ? Pas le moins du monde, et j’en veux pour exemple cette intégrale :

Qu’un amateur de mathématiques vienne me dire que cette formule n’est pas belle, je l’attends ! Cette intégrale, connue sous le nom d’intégrale de Gauss, est omniprésente en probabilité. En effet, ceux qui ont rencontré la loi normale se souviennent peut-être plus ou moins de sa densité ; pour une loi normale d’espérance μ et de variance σ, elle vaut :

J’en vois déjà crier victoire à la vue de ce 2π, mais attendez un peu : nous allons réarranger cette formule en posant S =√2σ :

Et voilà, envolé le 2π ! En réalité, le 2 ne se couplait pas avec le π ici, mais bien avec le σ.

Et de belles formules ne faisant intervenir que π, il y en a d’autres en réserves, et en voici un petit florilège rien que pour vos yeux ébahis.

Prenez donc la fonction Γ, définie ainsi pour tout x réel positif:

Cette fonction est bien connue puisqu’elle « généralise » la notion de factorielle. Nous avons les égalités suivantes :

Plus haut nous parlions de l’aire d’un disque, mais pourquoi se limiter à deux dimensions ? Regardons le volume d’une boule-unité dans un espace à n dimensions !

Allons maintenant voir la cousine : l’ellipse dont les demi-axes ont pour longueur a et b :

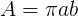
Et pour ceux qui aiment les intégrales, les fonctions trigonométriques mais aussi leurs réciproques nous donnent quelques jolies petites égalités :

Enfin, vous l’aurez compris, π a encore de beaux jours devant lui…

Et π c’est tout !

Pour compléter

• Les arguments avancés ici sont entre autres issus du Pi Manifesto

Toutefois, pour bien défendre son nombre, il faut savoir ce qu’on lui reproche !

• Bob Palais : π is wrong ! : http://www.math.utah.edu/~palais/pi.html
• Michael Hartl, Tau Manifesto : https://tauday.com/

Et du côté français :

• Aurélien Alvarez (Images des Maths), La valeur de π n’est pas la bonne : http://images.math.cnrs.fr/La-valeur-de-pi-n-est-pas-la-bonne.html
• Science4All, π est une fraude ! : https://www.youtube.com/watch?v=l8mVsmzmqfU